Carnot Cycle & Engines!

Here we are shown a PV graph and asked to find the W.

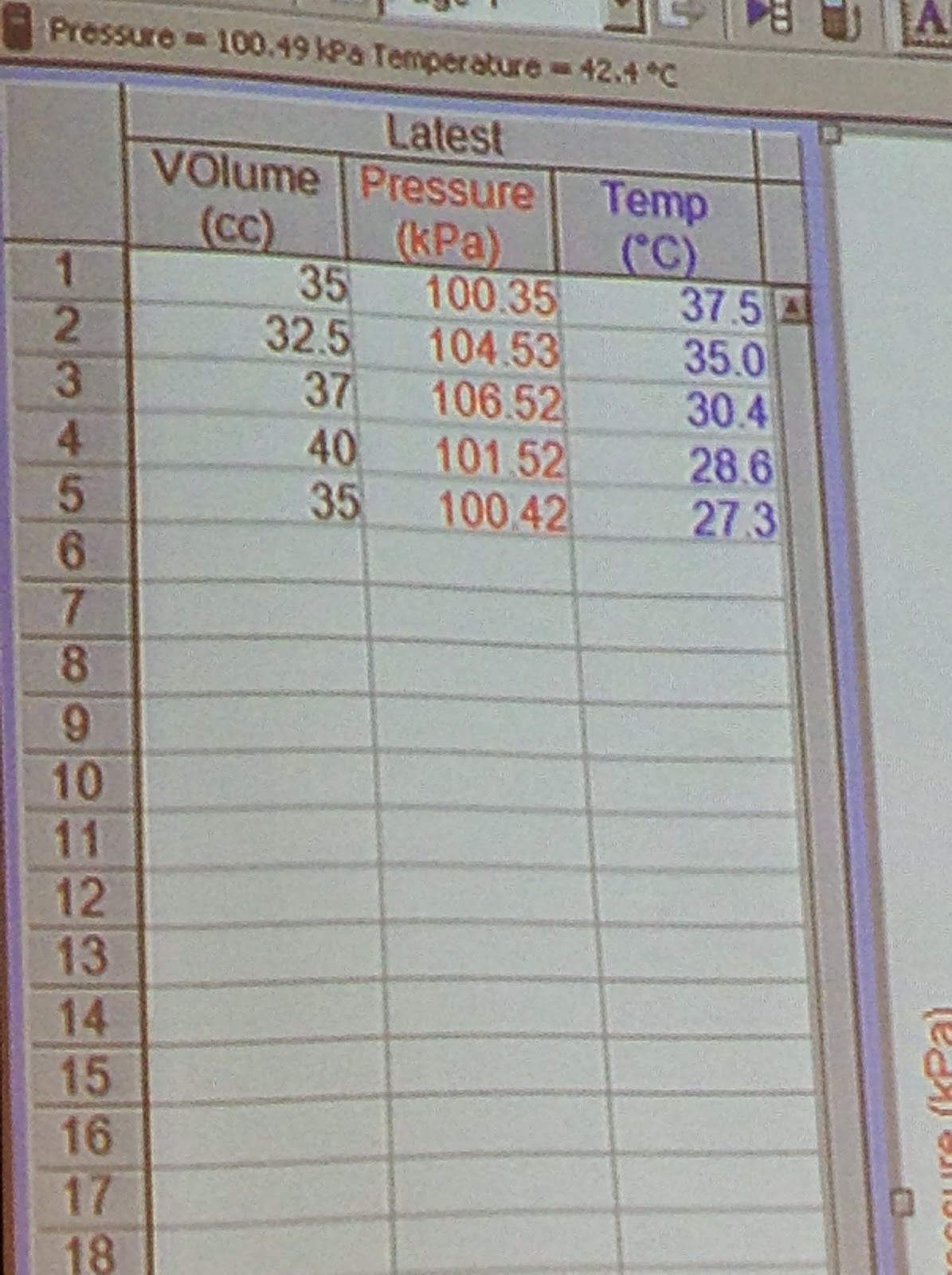Close up shot of Values

Unfortunately we were not able to solve for the W in class, however we did learn that work is the area in the shape. So we should have approached it by seperating the Graph into Trapezoids i would use 6 one from 32-35 the other from 35-37 and lastly 37-40, then i would subtract the bottom trapezoids giving us 6 in total.

Here we can use our definitions of internal energy work and heat, to solve for the constant Cp=5/2R.
We can also do the same for Cv by letting work = 0 and Q=nCvdelT giving us Cv=3/2R
Note: Cp-Cv=R

Here we have an adiabatic Expansion with small changes in pressure and volume. we use the chain rule to solve for ndelT, and then we substitute our Cp-Cv for R.using our Definition for adiabatic expansion we let Q=0 then set our definitions of Energy Internal to write a new equation. From here we set our two new equations equal to each other and take the the integral.

Now we can show relationships between P T and V. by using our ideal gas law PV=nRT.
Note: gamma = Cp/Cv

Using our new Formula for Pressure initial we can now solve for W=Spdv.

Here we solve for DelE Q and W by using our new formulas we just derived for the adiabatic expansion part of the carnot cycle. There were a few givens like Q=0 for adibatic and for Isothermal (U=3/2nKbdelT) Internal Energy is 0. From there we just used Wadiabatic to solve for W and E internal for two of the processes. The Isothermal Processes we used Eint = nCvdelT and then solved for W since Q=0. To find the efficiency of the system  we can W/Qh.

Quiz

Givens:

Work for P,V and T for points 1-4

Here i did it with n moles = 1, i did it another way as well but the number are ridiculous i will post it beneath

Givens and Work for Q,W and ΔU for all processes.

w=-80J and delU = 80J

In Conclusion, del U is not zero. but monday is over! 

Work for Thermal Efficiency.

Heat Engine and Cycles

A candle burning the oxygen and suffocating itself.

A candle burning the oxygen that it gets by induction which keeps the flame burning.

Top: Graph of an Isobaric Process where V and T are the only variables, notice how their is a linear correlation.
Bottom Left: Graph of an Isochoric Process where p and T are the only variables, and have a linear relationship.
Bottom Right: Graph of an Isothermal process where p and V are the only variables, and have an inverse relationship.

Now that we understand the relationship of the Isobaric, Isochoric and Isothermal Process, we can set up an equations where we have one pair of variables at time intial equal to those a t-final. By doing this we can just solve for whatever variable we did not measure or have originally!

Notice how we can find the pressure at any given volume, since we were given pressure and volume initial and were told n and T were constant. here we first solved the pressure at 20dm^3 then at 10dm^3.

PV graphs of isobaric, Isocholoric, Adiabaitc, and Isothermal Processes.

We solve for the work of gas by taking the integral of Pdv which gave us P_V_ln(V/V_).

Next we would solve for the W done by gravity which is (3/4)mgh for this specific case since the water tank was only 3/4 full of water. This also means that there is air in the tank, which means their is work being done by the air. The work air exerts is (1/4)*atmospheric pressure * 50. Once we add all of these values we finally get our answer or 1.793 *10^7 MJ.

Here we have a problem where Volume and Pressure are variables. So what we did was take the integral of P(v)dv but substitued nRT/V for P(v) which we can use an integral to describe its change since the only thing changing would be V. From there we can substitute PV back in or leave it as nRT. 

A PV graph was given to us which contained 4 points, the first thing we did was observe when work was being done by the gas(when P or V increase) and when work was being done on the gas(when P or V decrease). Then we went ahead and found the internal energy at each point which we describe to be equal to (3/2)PV.

From there what would be done is to label each of the sides A,B,C,D and let each side represent the change in internal energy which we could solve for by subtracting the final point from the initial point(like vectors). Finally we could find the Work done by using pdelV, then use the first law of thermodynamics to solve for Heat(Q). We could also solve for Worknet by adding the work from each side.

Here we have the efficiency of our system, which can be solved for by taking the ratio of Work over Heat added to our system.

Kinetic Theory and PV Diagrams

Here you can see we used the definition of velocity to find the velocity in one direction for  a single molecule. Then we can use the definition of F=dp/dt=mv-(-mv)/dt=2mv/dt, We the can double the time dtx= x/Vx(the time to get to the wall) so it get back to its original location. Finally we can say Fx=mVx^2/X.

Now we can go ahead and say F=P/A, therfore P=F/A which means P=Fx/X^2=mVx^2/X^3.
Now if we want to assumer there are N molecules all we have to do is multiple by N. We can also add other directions of freedom if we let Vx^2=Vy^2=Vz^2 we can say  Vtotal^2=3Vx^2.  and finally we can rewrite our expression for Pressure as P=NmVtotal^2/3V, or even once more as P=2N(Ekin)/3V. (notice how we let mVtotal^2=2(Ekin))

Now from the equation up above  we can say PV=2N(Ekin)/3 which we know is also equal to NkbT. We set them equal and we can find the velocity of the molecules. We can also find the a new equation by understanding the Eint can be defined as N(number of paticles) multiplies by the kinetic energy of each particle. doing this we find that Eint=3/2NkbT. On the left you see and isothermal compression where we find Q=W and on the right you see and adiabatic compression (dv=0)
 Eint = -W => 3/2nKdT=-pdV we take the integral and we find the C=T^3/2V

Solving the change in internal energy, First we solve for the Work needed to raise Temperature to 50 degrees Celsius from 20 degrees Celsius of a copper bar. Then we solve for Q which is equal to mcdeltaT which we find to equal 11.58kJ and then knowing  the first law of thermodynamics we get deltaE=Q-W = 11.58*10^3 J.

Here we use the equation derived above except instead of T^3/2V we use T^5/2V, this is because oxygen is diatomic and not mono-atomic. We got Tfinal = 604K or 628 degrees Fahrenheit, which we can compare to the 451 degrees needed to burn paper, which we learned in English! So we can expect the paper to burn! Don't believe me? video evidence below!

Gas Laws and First Law

When the hot can with steam inside made contact with the room temperature water it rapidly imploded, due to the low pressure in the can relative to the pressure outside.

We experimented with a balloon and a marshmallow as to what would happen if we decreased the pressure inside the the vacuum chamber, then let back to normal.

What hypothesized above was wrong,what happened was the marshmallow much like the balloon increased in size when the pressure decreased then rapidly shrunk to a size smaller than before when the pressure was normalized.

Here is a makeshift manometer. a manometer is an instrument that uses a liquid to measure pressure!

So each side has a pressure one is known as the applied pressure and the other is our atmospheric pressure. To find the hydro static we  use P=ρhg, however if we just want the pressure applied we can just subtract the reference pressure (atmospheric) pressure. We found that our applied pressure was 101026 Pa and that the mass or amount of water displaced was 5.3 * 10^-5

Here is how we think pressure and volume correspond! (which is wrong)

Here we saw Andrew pumping air into a pressure sensor!

We took measurements of the pressure sensor when at different volumes, every cubic centimeter  (cc)  you can see how the relationship of Pressure vs Volume is not linear but in fact are best described as inversely proportional.

Pressure Vs Temperature

This beautiful graph depicting the linear relationship between Temperature and Pressure.

If Volume is held constant you will see a linear relationship

Volume vs Temperature

Here we can see that as temperature increases the volume increases, which means they are linear.
The pressure of the air remains constant because, of the fact that Temperature and Volume are linear and as long as P=nRT/V, and volume and temperature can keep increasing pressure wont change.

As a balloon rises the gas expands! 

Here we solve for mass by multiplying molar mass by the number of moles in the hot air balloon(n=PV/RT)

now we can find the volume if no helium was lost during assent by setting pv/t=PV/T=nR since the number of moles is assumed to be constant and R is a constant.